Modeling and simulation of termination resistances in superconducting cables
by administrator on Mar 15, 2024 1:13:58 PM
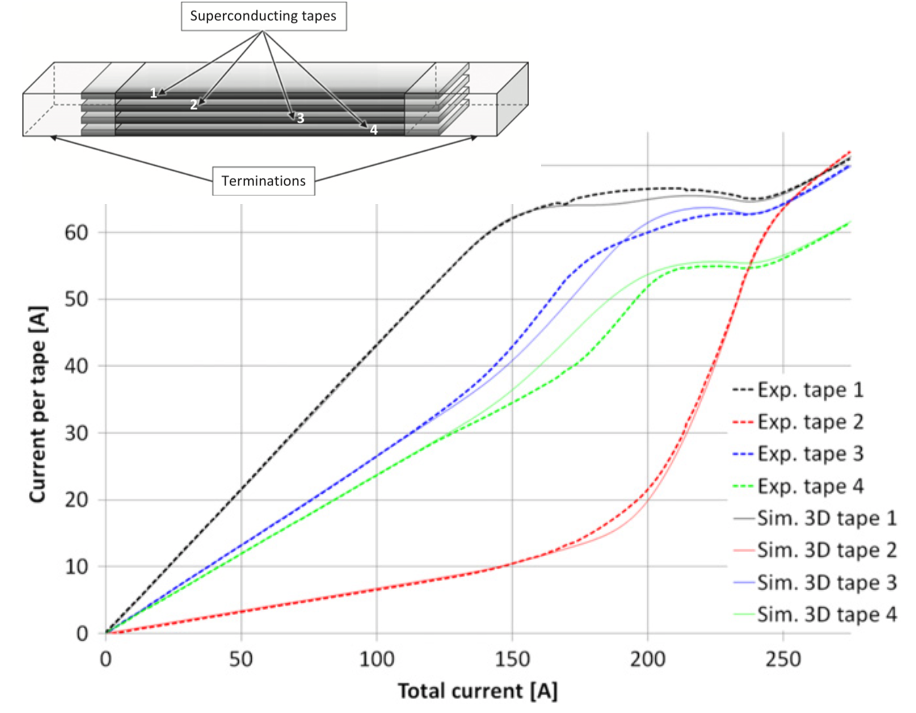
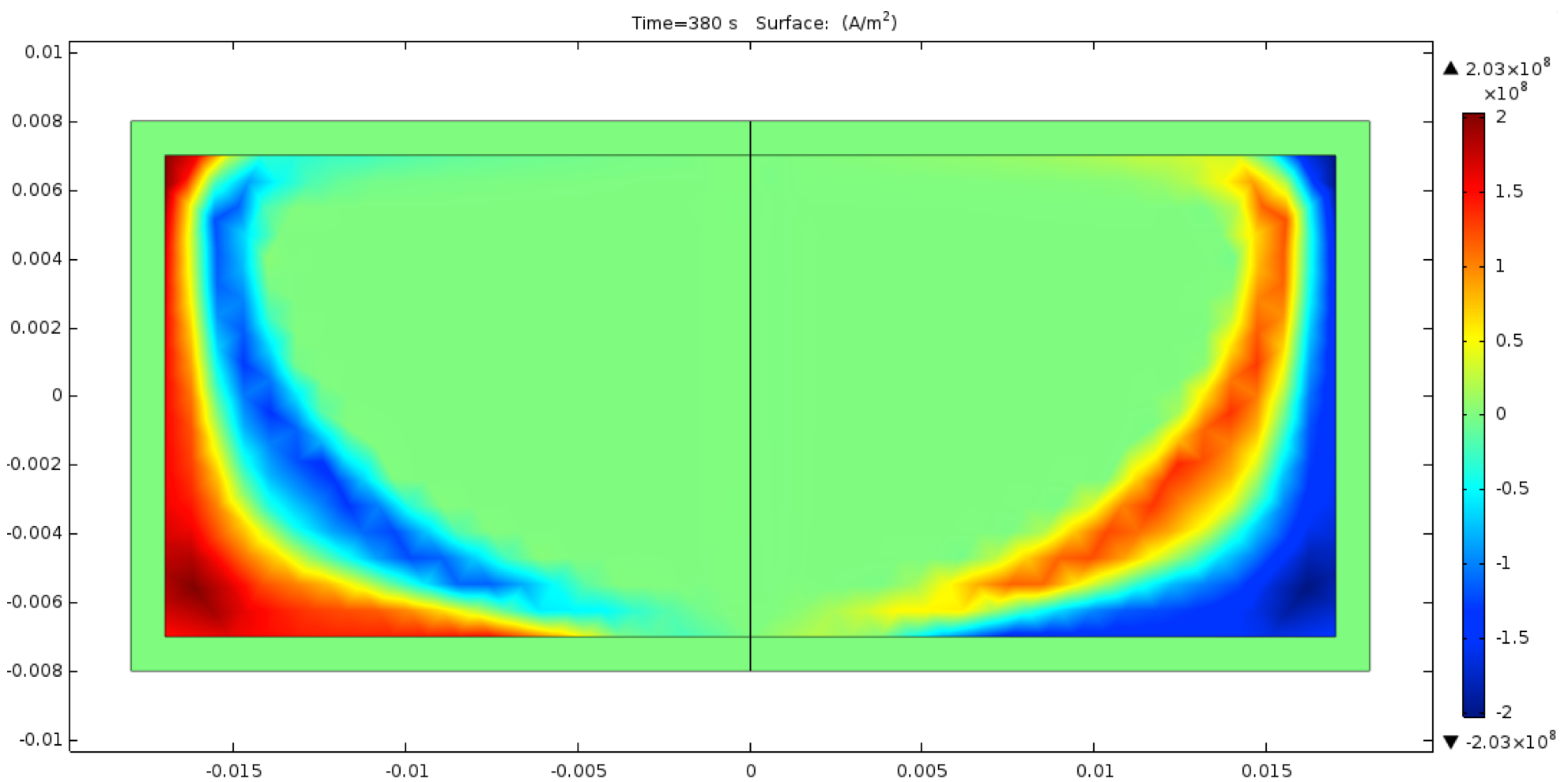
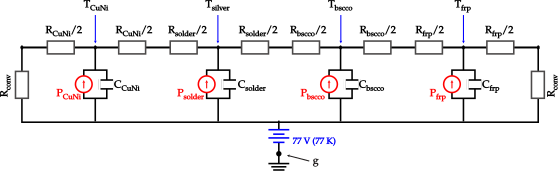
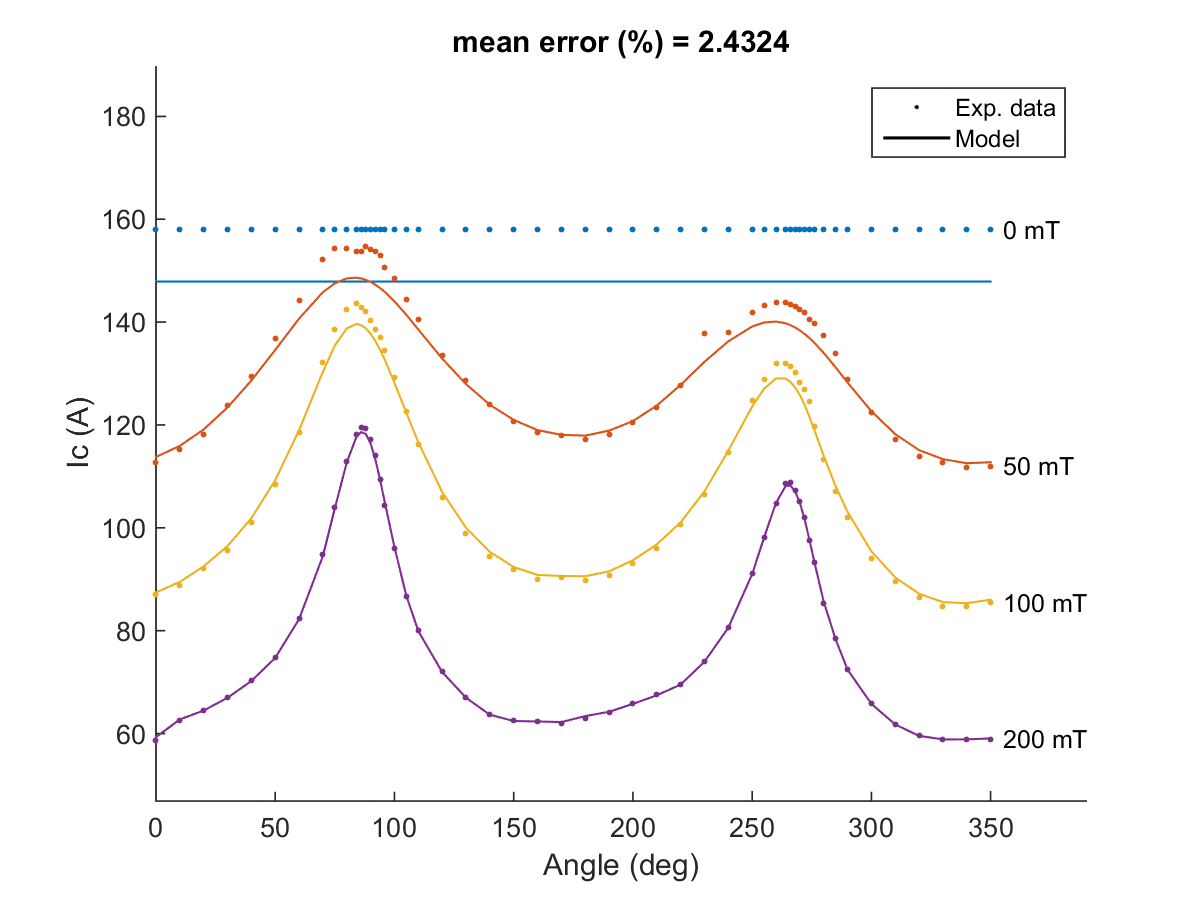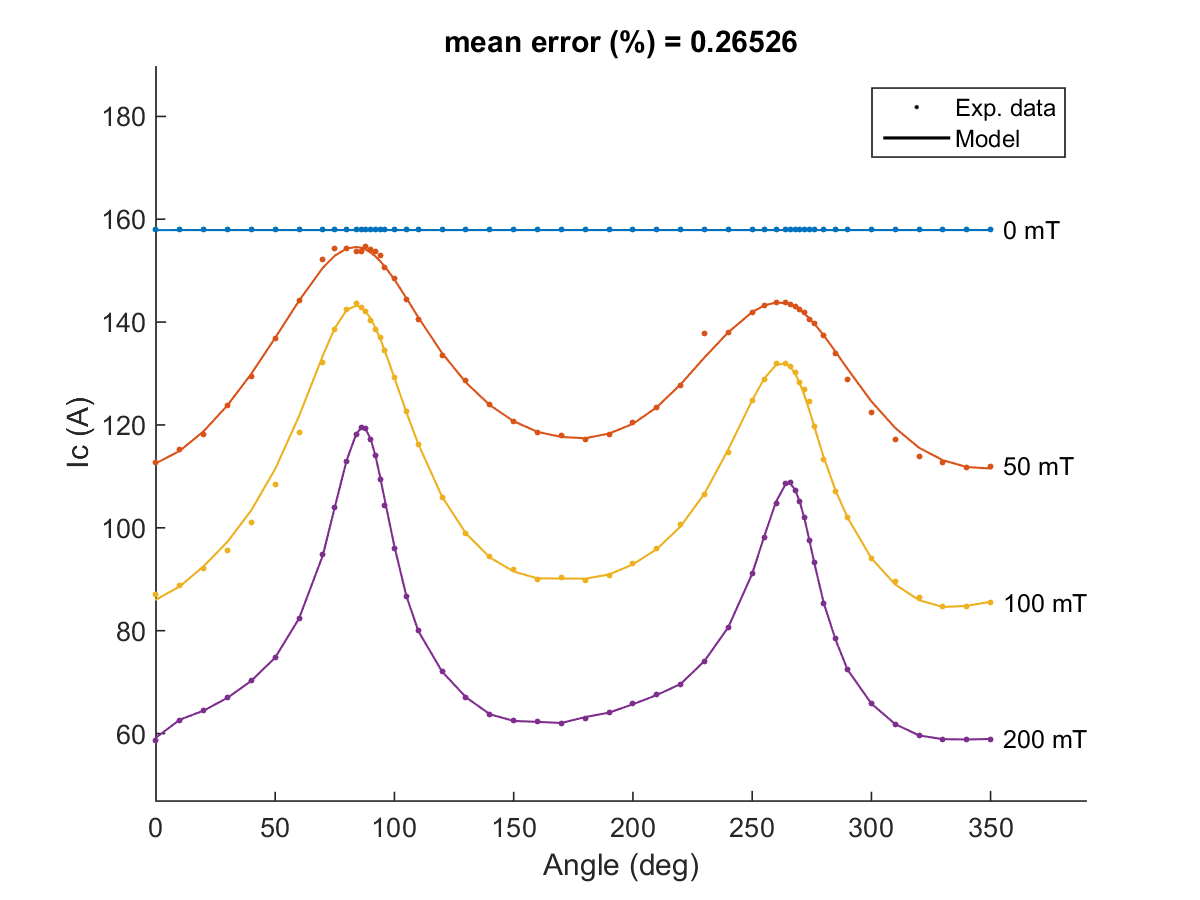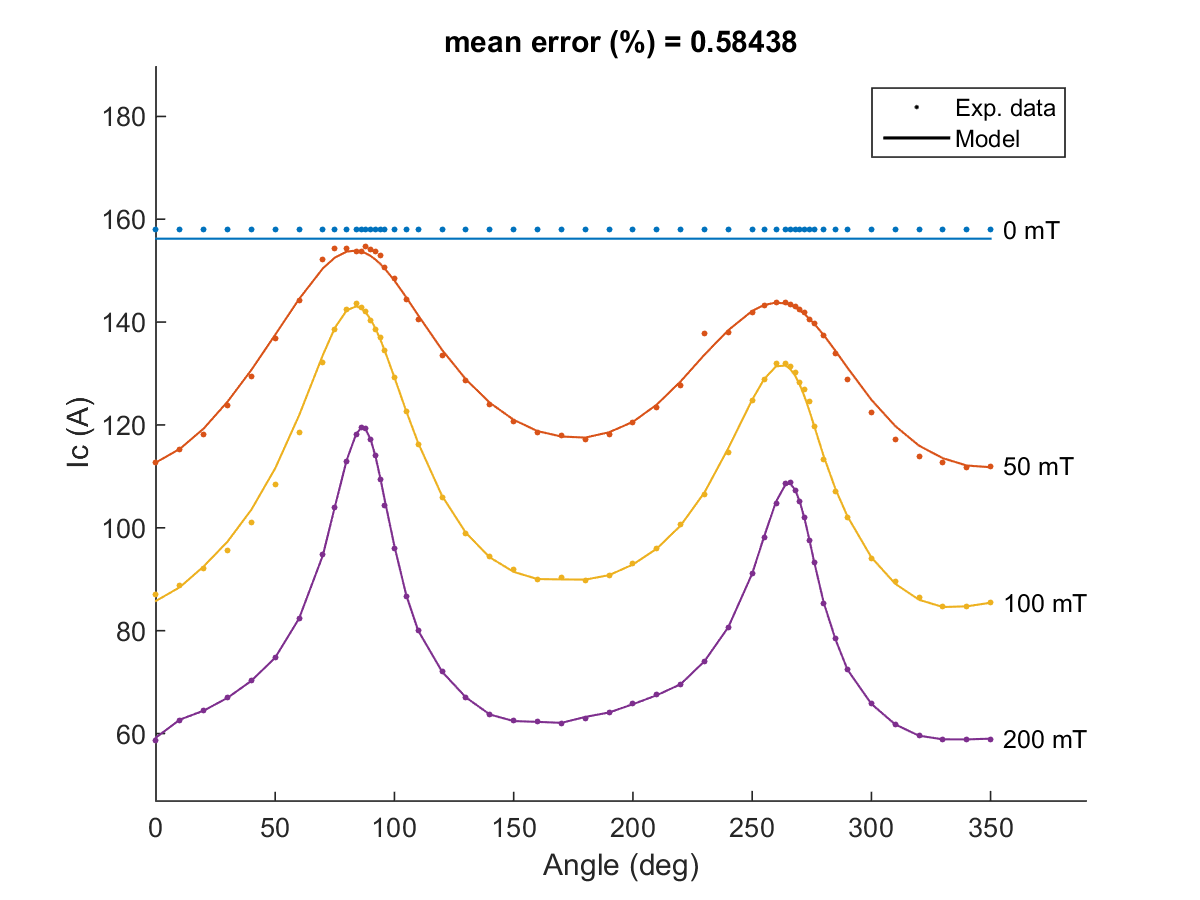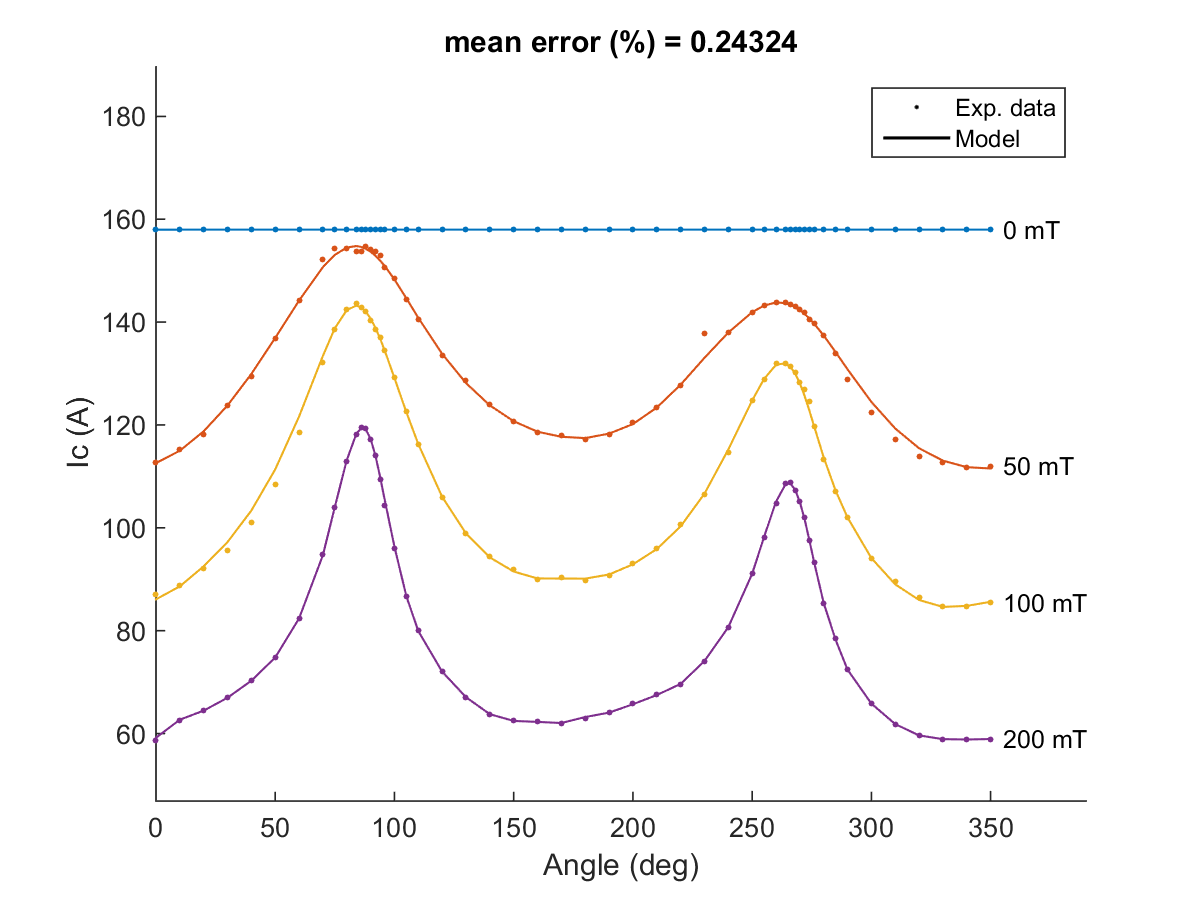
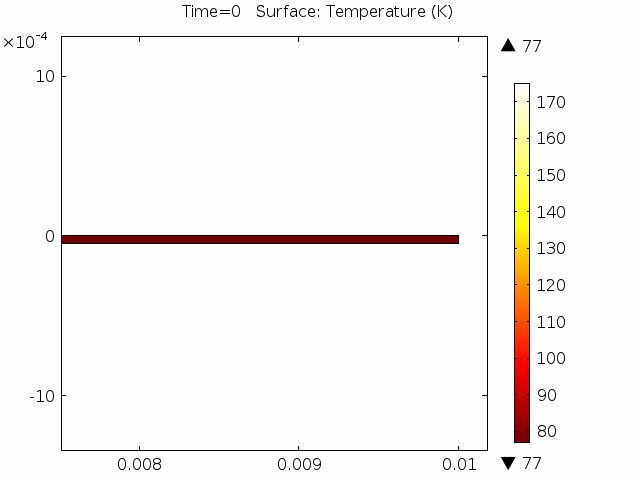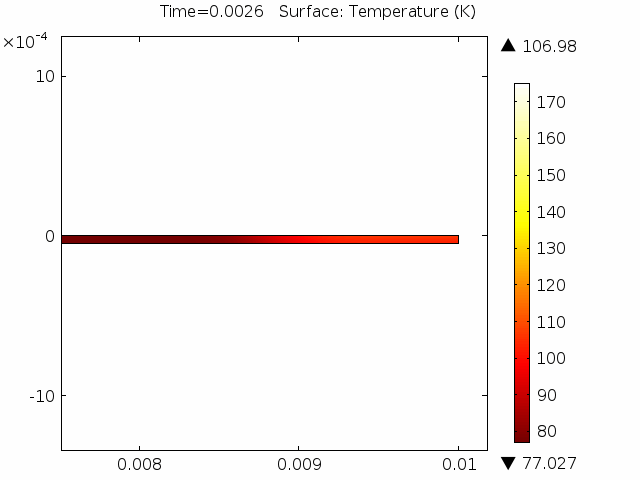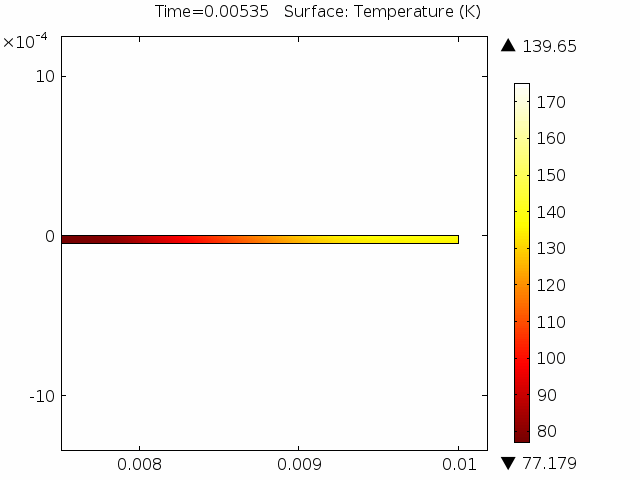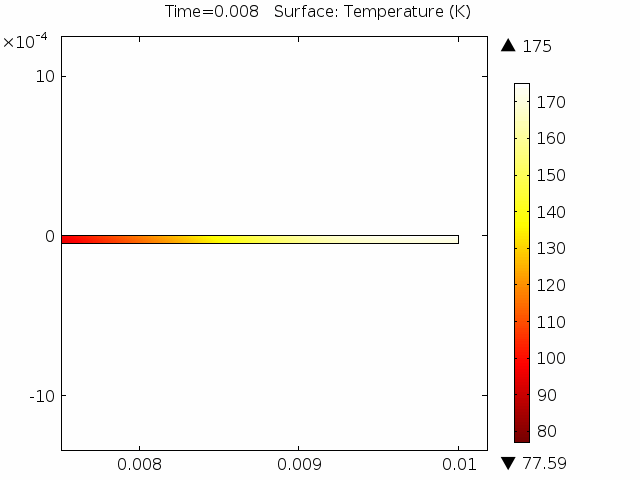
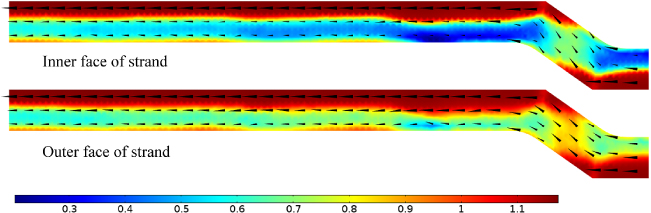
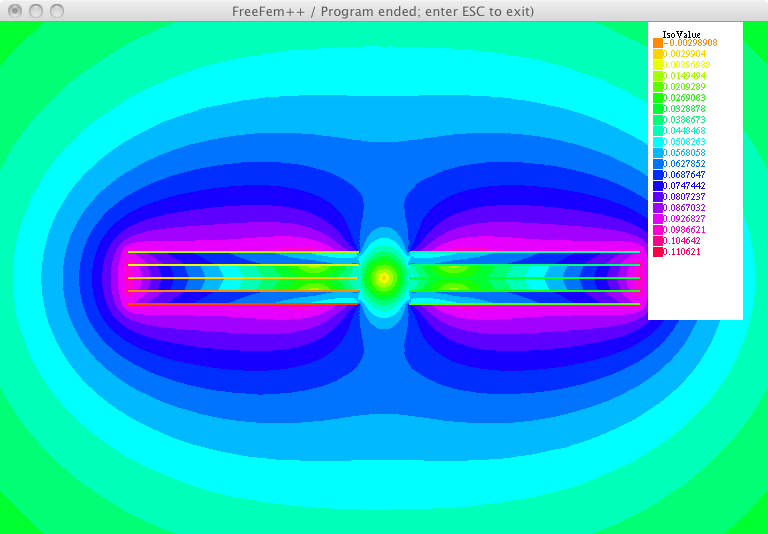
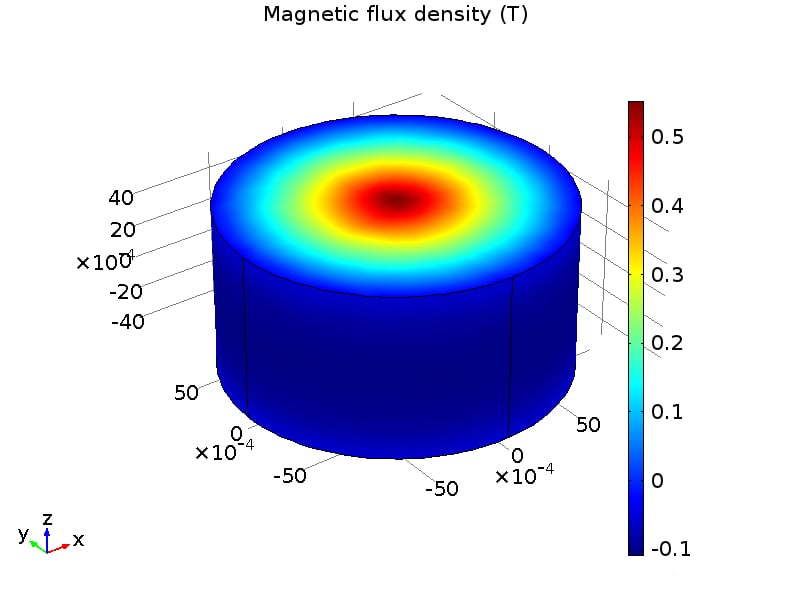
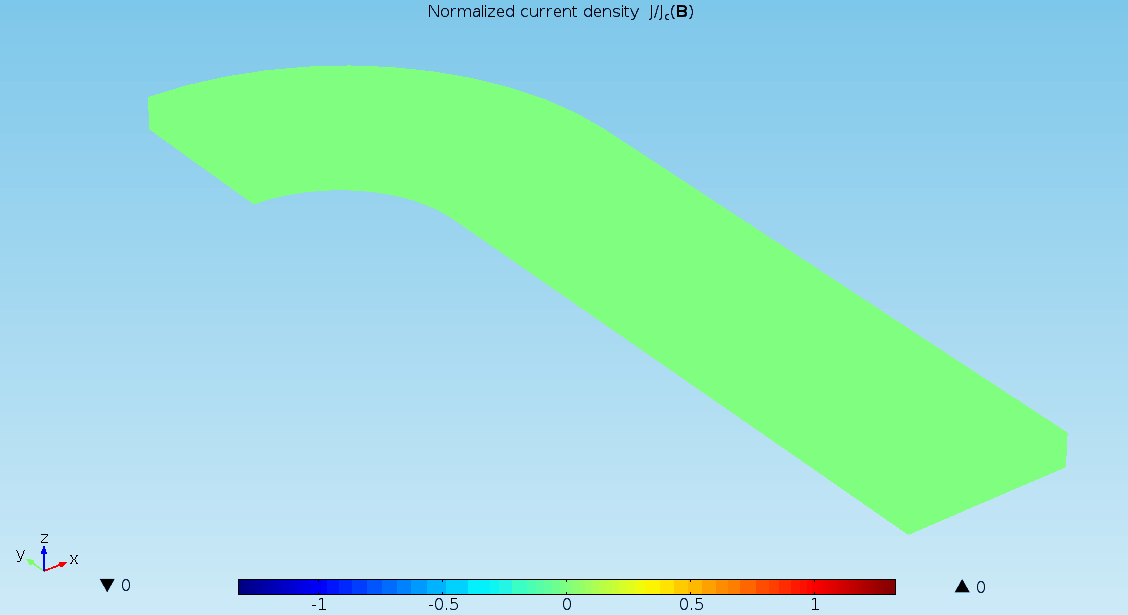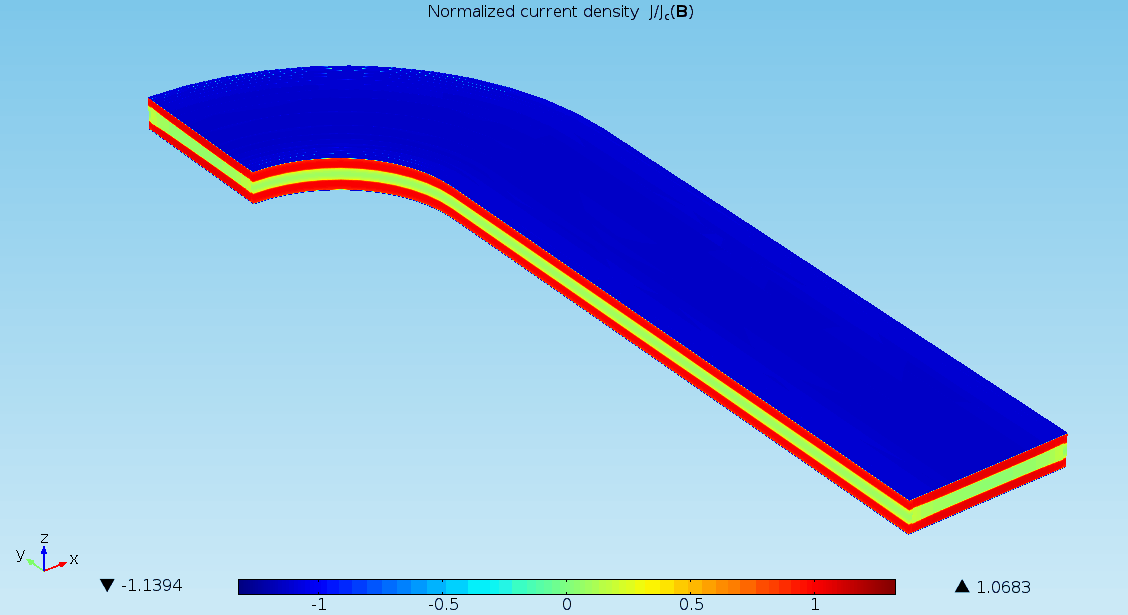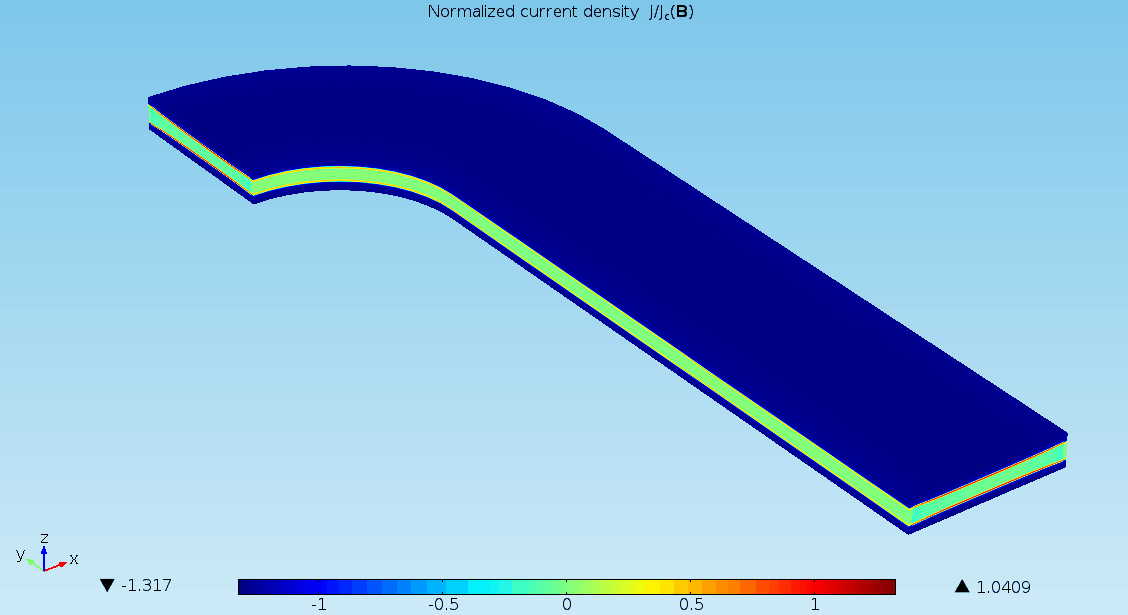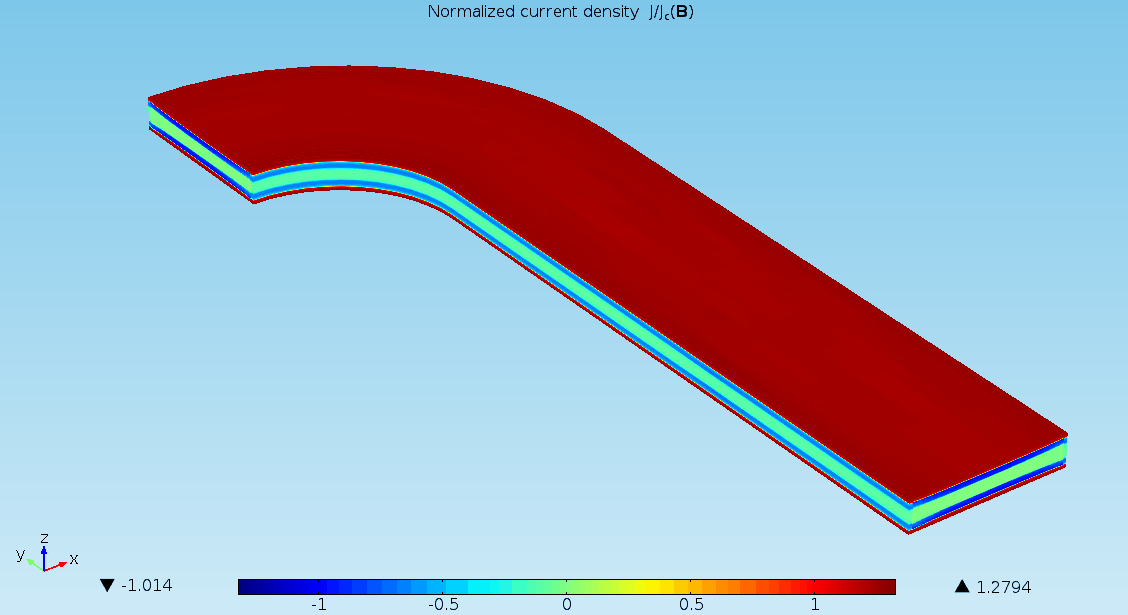
The models presented here are used to simulate termination resistances which are largely responsible for the uneven distribution of currents in superconducting cables [1]. For this purpose, four different models are presented. The first is a 0D stationary model, where time enters as a …
Superconducting magnetic bearing composed by a permanent magnet and bulk HTS sample
by administrator on Mar 15, 2024 1:11:12 PM
In the considered examples, the HTS sample is either a bulk superconductor or stacks of 2G wires. In the second case, the 2G stack was homogenized in order to speed up the solution. The movement between the HTS and the permanent magnet is avoided in the model by restricting the simula …
Superconducting fault current limiter (SFCL) connected to a power system
by administrator on Mar 15, 2024 1:08:33 PM
The model can be implemented in any power system simulator (e.g., Matlab/Simulink, EMTP, PowerFactoy, etc.) for transient analyses of short circuit currents. Here one presents the method applied to MCP-BSCCO-2212 SFCL devices. The method however has already been extended to SFCL based …
Parameter-free method to extract the Jc(B,θ) field-dependence from in-field current–voltage characteristics of HTS tapes
by administrator on Mar 15, 2024 1:00:34 PM
The method presented here allows computing the critical current density (Jc) of superconducting materials from its in-field experimentally measured critical current (Ic). This is particularly important for applications like HTS cables for power transmission and fault current limiters, …
2-D electro-thermal model for simulating non-uniform quench in 2G HTS coated conductors
by administrator on Mar 15, 2024 12:57:24 PM
The model calculates the time evolution of the electric potential and the temperature in a 2G HTS CC when a transport current is applied in presence of a low Jc region (defect) in the tape. The heat generated at the defect location creates a normal zone that propagates along the tape. …
Full 3-D time-dependent electromagnetic model for Roebel cables
by administrator on Mar 15, 2024 12:51:19 PM
This model was shared by V. Zermeno, Karlsruhe Institute of Technology. This model simulates the current distribution in the superconducting layers of a Roebel cable composed of 14 strands and estimates its AC losses. The mode is rather general and allows considering the cases of curr …
Self-consistent model to estimate the critical current of superconducting devices
by administrator on Mar 15, 2024 12:47:00 PM
This model was shared by V. Zermeno, Karlsruhe Institute of Technology. The model presented here is used to estimate the critical current of superconducting devices. Its implementation is very simple either using finite-element-based or general numerical analysis programs. The model r …
2-D axisymmetric and 3-D models for magnetization of superconducting bulks
by administrator on Mar 15, 2024 12:42:20 PM
Magnetic vector potential Current density distribution This model was shared by M. Ainslie, University of Cambridge. The first model is for a 2D axisymmetric bulk with zero field cooling (ZFC) magnetization. Here, the external magnetizing field is applied along the z axis – perpendicu …
2-D Campbell’s model to estimate magnetization losses in a wire in the critical state
by administrator on Mar 15, 2024 12:21:44 PM
Magnetic vector potential Current density distribution This model was shared by E. Rizzo. The model calculates the penetration of the magnetic field in the cross-section of a superconducting wire in the critical state subjected to a transverse magnetic field.
3-D homogeneous model to estimate AC losses in coated conductor stacks and coils
by administrator on Mar 15, 2024 12:18:58 PM
This model was shared by V. Zermeno, Karlsruhe Institute of Technology. This model uses a homogenization technique to calculate the current distribution inside the superconducting layers of a racetrack coil and to estimate its AC losses.